Giáo Dục

The mind is like a parachute. It only works when it opens

(Frank Zappa)

Có một tỷ phú “nịnh đầm” nói với người yêu thế này: “Trước khi gặp em anh chỉ là một dãy gồm một chục con số 0, đến khi gặp em thì em là số 1 đứng đầu dãy số 0 đó.” Ngày nay chúng ta đều thấy sự cần thiết của số Không, hay zero, hay 0 và coi như chuyện đương nhiên khi sử dụng con số này. Chưa hết, tuần dương hạm USS-Yorktown trong một chuyến hải hành ngoài khơi Cape Charles, Virginia, ngày 21 tháng 9, 1997 bất thình lình bị hoàn toàn bất khiển dụng vì hệ thống computer điều hành chiến hạm ngưng hoạt động. Hệ thống computer ngưng hoạt động vì một kỹ thuật viên đã sơ suất để cho computer chia cho số 0. Chia cho số 0 là điều tối kỵ trong toán học, không phải là một lỗi lầm (mistake) nữa mà là một “tội lỗi” (sin). Computer khi làm đến con toán này bị bí và cả hệ thống cứ chạy vòng vòng, điều mà chúng ta vẫn hay thường nói là computer của tôi bị treo giò (hang up). Thế là một chiếc tuần dương hạm tối tân, trang bị hoả tiễn đạn đạo có radar hướng dẫn, không bị đánh mà vẫn bị “chìm,” phải chờ tàu kéo vào bờ sửa (Seife, 2000). Bài viết dưới đây trình bày sơ lược lịch sử sự hình thành và phát triển của số zero và sự đóng cứng của não trạng đã phủ nhận sự hiện hữu của zero và kềm hãm sự tiến hoá của thế giới Tây phương trong hơn 2000 năm.

Lịch sử các con số 

Trước khi bàn về sự xuất hiện và tác dụng của con số Không, chúng ta hãy đi ngược về quá khứ và tìm hiểu xem những con số mà ta đang sử dụng ngày nay được con người sáng tạo ra từ bao giờ và để làm gì. Trước khi phát minh ra con số, con người đã biết đếm rồi. Nhà khảo cổ Karl Absolom đào được, từ cuối thập niên 1930, ở Tiệp Khắc một miếng xương chó sói, có số tuổi 30,000 năm trước, trên có khắc những vạch. Không ai biết người tiền sử ở thời đại Đồ Đá đó vạch những vạch đó vào việc  gì, nhưng có điều chắc chắn là người ấy đang đếm một cái gì đó (Seife, 2000). Trên khúc xương này có 55 vạch, được xếp theo từng nhóm 5 vạch một; sau 25 vạch lại có thêm một vạch, ta có thể đoán là người đó đếm theo hàng 5 chứ không phải theo hàng chục. Tại sao lại là con số 5? Không ai biết được. Có lẽ tại trời sinh ra con người với năm ngón tay chăng? Nếu người đó đếm theo hàng chục thì ta có bằng chứng về hệ thập phân (Seife). Ở Nam Mỹ đã có bằng chứng khảo cổ về hệ thống nhị phân (Conan, 1896). Người Pháp chắc đã có thời dùng hệ nhị-thập phân, như con số 80, người Pháp đọc và viết là quatre-vingt (bốn lần 20). Nhưng hệ thống những con số được xem là tiến hoá từ hệ thống của Ai-cập với những con số tượng hình[1] (hieroglyphic) dùng hệ thập phân, mãi từ 3000 năm trước Công nguyên (TCN). Cũng khoảng từ 3000 năm TCN, người Sumerian sống ở khu vực Lưỡng Hà (Euphrates và Tigris thuộc Iraq ngày nay) cũng phát minh ra hệ thống số lục thập phân (sexagesimal), hệ thống số của người Sumerian dùng biểu tượng đặc biệt cho các con số 1, 10 và 60. Khi thành Babylon phát triển thì sức hút của thương mại và văn hoá đã thu hút người Sumerian và hệ thống số Sumerian được dùng rộng rãi ở Babylon và sau này được biết đến là hệ thống số babylon (Weibull).

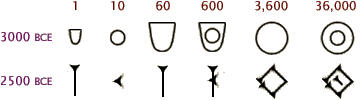
Hình 1: Số Sumerian

Người Ai-cập dùng số và toán học vào những việc thực tế, thí dụ như toán nhân là tìm diện tích của hình chữ nhật hay tam giác. Sự phát triển của số học và hình học tại Ai-cập một phần cũng là vì một sự tình cờ của địa lý, vì hàng năm con sông Nile vẫn dâng nước làm ngập lụt đất đai và mất luôn cả ranh giới đất đai của dân cư. Điều này khiến các ông vua pharaoh phải cử các quan điền sứ đo đạc đất đai để làm căn cứ so sánh. Toán học Ai-cập đã phát triển đến mức không những chỉ tìm diện tích mà còn tìm cả thể tích, như thể tích của những kim tự tháp. Trình độ toán học của Ai-cập lừng danh cả miền Địa-trung-hải, các nhà toán học nổi tiếng của Hy-lạp như Thales và Pythagoras đã sang học ở Ai-cập.[2] Tất cả mọi học sinh trung học đều biết định lý Pythagoras: “Trong một tam giác vuông, bình phương cạnh huyền bằng tổng số bình phương hai cạnh kia.” Khi Ai-cập bị Ba-tư xâm chiếm và Pythagoras cũng bị bắt làm tù binh và đưa sang Babylon (O’Connor & Robertson, 1999), có lẽ trong lúc ở đó Pythagoras tiếp thu được hệ thống số của người Babylon.

Khi trở về Hy-lạp, Pythagoras sáng lập một môn phái vừa mang tính triết học, vừa mang tính tôn giáo. Có hai loại giáo đồ; giáo đồ xuất thế và nhập thế. Giáo đồ xuất thế đều ăn chay trường, không sở hữu một thứ gì hết, và ở chung trong tu viện. Giáo đồ nhập thế sống ở nhà riêng (giống như tu tại gia), không phải ăn chay trường, và được sở hữu tài sản. Giáo đồ xuất thế được gọi là mathematikoi; với danh xưng này hiển nhiên, toán học là điểm trọng yếu trong pháp môn tu tập của họ (O’Connor et al). Pythagoras đã có câu nói trứ danh “Vũ trụ được điều hành bởi những con số.” Theo tiếng Hy-lạp, tỷ số(ratio)[3] còn được viết là logos, và vào thời đó, con người chỉ mới biết đến số nguyên (whole number), và tỷ số là một phân số của hai số nguyên, thí dụ 2/3, 8/11, vân vân. Những con số này còn được gọi là số hữu tỷ, và những con số này vận hành vũ trụ của những người theo phái Pythagoras một cách hài hoà. Sự hài hoà của vũ trụ, ở trên trời qua sự vận hành của những hành tinh, và ở dưới đất qua những hình dáng vật thể, được thể hiện qua tỷ lệ vàng (golden ratio), cân đối, toàn mỹ. Đền đài, dinh thự, ảnh và tượng đều được xây dựng theo tỷ lệ này, thí dụ như điện Parthenon ở Athen, ta thấy được tỷ lệ vàng này được thể hiện ở mọi nơi của công trình; còn ở trong thiên nhiên, tỷ lệ vàng thể hiện trong cấu trúc vòng xoắn của vỏ ốc và trái dứa (Seif, 2000). Thế thì tỷ lệ vàng là cái gì? Hãy chia một đoạn thẳng làm hai phần không bằng nhau sao cho tỷ lệ của phần nhỏ đối với phần lớn bằng với tỷ lệ của phần lớn đối với cả đoạn thẳng.[4] Sau một hồi tính toán ta sẽ tìm ra được tỷ lệ này vào khoảng 0.618, hay vào khoảng 3/5. Có lẽ đây cũng là lý do mà ta thấy những tấm index card hay hình ảnh ở Mỹ có kích thước tiêu chuẩn 3 x 5 hay 4 x 6. Chính vì niềm tin vào những con số, một câu chuyện thương tâm đã xảy ra.

Truyền thuyết kể rằng Hippasus, người xứ Metapontum, bị kết tội tử hình bằng cách dìm xuống nước, chỉ vì Hippasus, một môn đồ phái Pythagoras đã phát hiện ra một bí mật mà sẽ làm đảo lộn trật tự vũ trụ của phái này. Theo định lý Pythagoras, bình phương cạnh huyền bằng tổng số bình phương hai cạnh kia. Giả sử có một hình tam giác vuông cân với hai cạnh có chiều dài bằng 1, thì cạnh huyền sẽ có chiều dài là căn số của 2, . Khổ nỗi không phải là 1 vì 1 nhân 1 vẫn bằng 1; cũng không phải là 2, vì 2 nhân 2 bằng 4. Như vậy có một con số không phải là số nguyên, và không thể được diễn tả bằng một tỷ số của hai con số nguyên, xuất hiện trong vũ trụ của giáo phái này. Bí mật này không thể bị tiết lộ ra ngoài, vì sự thật này sẽ tiêu diệt cái raison d’être của cả giáo phái. Và thế là Hippasus phải chết để bảo toàn bí mật (Clegg, 2011).

Người Hy-lạp phát minh ra hệ thống con số vào khoảng năm 500 TCN, dựa theo ký hiệu số của Ai-cập, nhưng dùng mẫu tự thay cho con số theo bảng dưới đây:

Bên Đông phương, người Hoa cũng đã sáng chế ra hệ thống con số của họ vào khoảng 2500 TCN; các học giả nhận định rằng người Hoa sáng chế ra hệ thống con số của họ hoàn toàn cách ly với thế giới bên ngoài (Weibull). Hệ thống số của Trung Hoa gồm các con số từ một đến 9 (nhất, nhị, tam, tứ,…, cửu), và bội số của 10 (thập), 100 (bách), 1000 (thiên), 10,000 (vạn). Thí dụ, số 75,000 sẽ được viết thành thất vạn, ngũ thiên (七万五千).

Ngoài ra, kể từ đầu Công nguyên, còn có hệ thống số La-mã, dùng mẫu tự để chỉ con số như số 1 La-mã là I, số 4 là IV, số 5 là V, số 9 là IX, và số 10 là X, 50 là L, 100 là C, 500 là D, và 1000 là M (1975 viết bằng số La-mã sẽ là MCMLXXV). Khoảng 400 năm TCN, thổ dân Maya ở Nam Mỹ phát triển hệ thống số của họ. Đặc biệt là người Maya đã phát minh ra con số zero (Weibul)

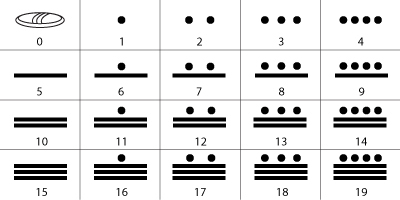
Hình 3: Số của người Maya

Cũng vào khoảng bốn, năm trăm năm TCN, hệ thống số Ấn-độ (Hindu) được nhà thiên văn học lừng danh Âryabhata và đệ tử là Bhâskara I phát minh ra theo hệ thập phân. Tưởng cũng cần nói thêm là người Hindu đã sử dụng số zero từ trước, nhưng chỉ từ khi hai nhà thiên văn này phát triển hệ thống số Hindu và thêm vào con số zero, thì hệ thống số Hindu mới được coi là tạm hoàn chỉnh (Weibull). Hệ thống số Hindu dần dần được người Ả-rập sử dụng vào khoảng thế kỷ thứ 9 sau công nguyên. Nhà toán học Ba-tư, al-Khowârîzmî, được xem là nhà toán học Ả-rập tiên phong sử dụng và cải biến hệ thống số Ấn-độ. al-Khowârîzmî cũng là người đã sử dụng lần đầu tiên từ “algorithm” và “algebra,” và trong tác phẩm Tính toán bằng số Ấn-độ, viết năm 825, al-Khowârîzmî đã giới thiệu hệ thống số Ấn-Ả rập với Tây phương, và từ đó chúng ta có những con số sử dụng ngày nay, kể cả số zero.

Số Không, Cái Không và Vô Cực

Như trên đã trình bày, kể từ khi con người phát minh ra các con số từ hơn 3000 năm về trước, con người không cần con số Không (zero), vì nó chẳng dùng được vào việc gì thực tế cả (không có con bò, hay không có miếng đất, thì đâu cần ghi lại làm gì?) Dù con số Không chẳng dùng được vào việc gì thực tế, chẳng thế mà lịch sử hình thành các con số từ đông sang tây đều cho thấy con số zero không được con người phát minh ra. Nhưng khái niệm về cái Không (emptiness) đã được triết học Đông phương chấp nhận như một phần không thể thiếu của nhận thức luận. Các nền triết học tại Đông phương như Ấn-độ, Trung Hoa, Nhật và các tôn giáo như Ấn giáo, Phật giáo, Đạo giáo,[5] đều quan niệm cái Không không phải là không mà là một sự hiện hữu tự nhiên (Liu & Berger, 2014). Ta vẫn thường nghe câu nói quen thuộc của đạo Phật “sắc sắc, không không” để chỉ sự vô thường của vũ trụ, của hiện tượng thiên nhiên, ngay cả của kiếp sống con người. Về phương diện triết học, theo Phật giáo cái Không chỉ sự giả hợp, những sự trình hiện của hiện tượng. Khổng tử  (sinh năm 479 TCN) cũng thế, cho rằng vạn vật đều luân chuyển, cái có đấy thì cũng mất đấy, như trong câu nói “thệ giả như tư phù, bất xả trú dạ,” dịch nghĩa: “Vật như sông nước cùng trôi, Ngày đêm chuyển dịch chẳng ngơi, chẳng ngừng” (Luận ngữ, thiên Tử Hãn).

Thế còn về phương diện vật lý thì sao, có cái gì thực sự là không hay không? Để trả lời câu hỏi này, có lẽ ta phải dùng tới Định luật Hạ nhiệt (Law of Cooling) của Newton: “Tỷ lệ thay đổi nhiệt độ của một vật tỷ lệ thuận với sự khác biệt giữa nhiệt độ của vật đó và nhiệt độ của môi trường xung quanh.” Dưới dạng phương trình định luật này là y(t) = Ce^(kt) + Ts, trong đó y(t) là nhiệt độ của vật tại thời điểm t, T_s là nhiệt độ của môi trường xung quanh. Giả sử ta có một ly nước sôi 100⁰ C đặt trong một căn phòng có nhiệt độ là 21⁰ C (khoảng 70 độ F), để cho ly nước sôi này nguội bằng nhiệt độ căn phòng cần bao nhiêu tiếng đồng hồ, nếu sau 30 phút, ly nước giảm xuống còn 95 độ? Nếu ly nước giảm nhiệt độ xuống bằng nhiệt độ căn phòng, thì phương trình trên sẽ thành Ce^kt = 0 và không thể giải được vì không thể lấy log của zero. Tuy nhiên, nếu thay vì đòi hỏi nhiệt độ của ly nước phải tuyệt đối bằng nhiệt độ căn phòng, ta chỉ cần nhiệt độ này gần bằng nhiệt độ căn phòng, thí dụ, 21.01, hay 21.001, hay 21.000000001 (một phần tỷ), thì ta có thể tính được khoảng thời giờ cần thiết (khoảng 5 tiếng) nhưng nhiệt độ của ly nước chỉ có thể tiến gần đến nhiệt độ căn phòng, chứ không bao giờ đạt được nhiệt độ 21 độ cả. Thế thì cái Không là cái gì, con số zero là cái gì? Có cái thật là không hay không, hay chỉ là một khái niệm của tâm trí con người, một ảo ảnh (a phantom of the mind)? Một thí dụ nữa là nghịch lý Zeno. Zeno, một triết gia Hy-lạp sinh vào khoảng thế kỷ thứ năm TCN, chứng minh rằng Achilles (người hùng trong trận chiến thành Troy) không bao giờ có thể đuổi kịp con rùa bò trước một khoảng cách, cho là một trăm thước. Nếu vận tốc của con rùa bằng một nửa vận tốc của Achilles, khi Achilles chạy đến mốc 50 thước, thì con rùa cũng đã bò được một khoảng 25 thước. Giả sử thêm rằng vận tốc của con rùa chỉ bằng một phần mười vận tốc của Achilles. Khi Achilles chạy đến mốc 100 thước, thì con rùa cũng đã bò được một khoảng 10 thước. Khi Achilles chạy 10 thước nữa, thì con rùa cũng đã bò lên phía trước thêm 1 thước, và cứ thế khi Achilles vượt được một khoảng cách, thì con rùa cũng bò thêm được một khoảng cách, và những khoảng cách này là vô tận (thí dụ, một nửa của một nửa, và cứ thế… ad infinitum). Rút cục, Achilles không thể nào đuổi kịp con rùa! Nói một cách khác, khoảng cách càng nhỏ lại đến gần zero, thì thời gian lại càng dài ra…đến vô cực. Cái Không và cái vô cùng (vô cực) có liên hệ mật thiết với nhau. Ai cũng biết là không chia được một số cho số Không, nhưng nếu ta chia số đó cho một số rất nhỏ, gần bằng zero (1 phần ngàn tỷ chẳng hạn), kết quả sẽ là một số cực lớn mà vẫn thường được các nhà toán học gọi là vô cực (infinity).

Trong thế giới vật lý, cái Không là một “cái” quan trọng mà nếu không có nó, thì có lẽ thế giới vật chất cũng không thể tồn tại được. Nếu cái ly không có cái Không, thì nó không thể đựng được nước hay chất lỏng; cái nhà không có cái Không, thì ta không có chỗ ở; vũ trụ không có cái Không, thì con người ở vào chỗ nào. Người viết còn nhớ khi được giới thiệu lần đầu tiên đến tân toán học (hình như năm lớp 9 thì phải) về tập hợp trống. Ông thầy đã định nghĩa thế này: “tập hợp trống là tập hợp không có gì ở trỏng, và tập hợp trống luôn luôn là phần tử của mọi tập hợp.” Cái có và cái không phải chăng luôn luôn tồn tại song song?

Sự đóng cứng của não trạng

Đối với người cổ Ai-cập và Hy-lạp, cái ý niệm về một khoảng trống là một sự kiện khủng khiếp, vì họ tin rằng vũ trụ được tạo ra từ khoảng không, đen tối, hỗn độn, và phải trải qua một thời gian dài mới được thần Atum, chủ tể của vũ trụ ổn định trật tự. Hậu duệ của Atum là Osiris và Set tiếp tục công trình ổn định trật tự của vũ trụ cho cân bằng và hài hoà (Mark, 2013). Vì thế, người cổ Ai-cập và Hy-lạp từ khước cái khoảng không gian đen tối, hỗn độn và đáng sợ đó. Họ chấp nhận rằng vũ trụ là một thực thể hữu hạn, chứ không thể vô hạn và tiến tới vô cùng vô tận (infinity) được. Aristotle, một vĩ nhân, phải nói là của cả nhân loại,[6] đề ra một mô hình vũ trụ, trong đó không có khoảng không vô tận, mà gồm những quả cầu đồng tâm trong suốt như pha lê, có tâm là trái đất của chúng ta, và trái đất đứng yên, không chuyển động, các hành tinh chuyển động quanh trái đất (mô hình địa tâm, geocentrism) (Mastin, 2009).

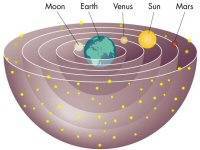
Hình 5: Mô hình địa tâm

Mô hình địa tâm của Aristotle được công nhận vì nó giải thích được những hiện tượng thiên nhiên mà con người quan sát. Trong vũ trụ của Aristotle, vô cực, và số zero không có chỗ dung thân. Mô hình địa tâm được phát triển ra toàn thế giới thời ấy có lẽ vì Đại đế Alexander, một vị vua lừng lẫy của Hy-lạp, người đã chinh phục toàn cõi Địa trung hải, Tiểu Á, Ba-tư, sang đến cả Ấn-độ, và qua những chiến thắng này Đại đế Alenxander cũng đem tư tưởng và học thuật Hy-lạp đến những nước bị xâm chiếm. Tưởng cũng cần nói thêm Alexander là học trò của Aristotle nên dĩ nhiên muốn phổ biến tư tưởng của thầy mình cho toàn thế giới. Khoảng hai trăm năm sau Aristotle, Claudius Ptolemy, nhà thiên văn học xứ Alexandria hoàn thiện mô hình địa tâm khiến cho mô hình này trở thành mô hình tiêu chuẩn của thiên văn học Tây phương trong hơn 2000 năm. Một hệ luận nữa của mô hình địa tâm của Aristotle khiến cho mô hình này đứng vững suốt 2000 năm là vì nó lý giải sự hiện hữu của Thượng đế. Aristotle lập luận như thế này: những thiên thể quay quanh trái đất tạo ra những hiện tượng mà ta quan sát được; như vậy, theo định luật nhân-quả, phải có một cái gì đó làm những thiên thể này chuyển động. Trái đất tĩnh tại không thể là nguồn của động lực này. Do đó, thiên thể ở trong cùng phải bị thiên thể ở bên ngoài làm chuyển động, và cứ thế ra đến thiên thể cuối ở ngoài cùng (vũ trụ hữu hạn). Thiên thể cuối cùng này phải được một lực nào đó làm chuyển động. Aristotle gọi đó là động lực thái sơ (prime mover) và đó chính là Thượng đế (Seife, 2000). Mô hình vũ trụ địa tâm của Aristotle trở thành mô hình thống trị trong hai ngàn năm vì khi Thiên Chúa giáo được truyền bá khắp Âu châu đã nồng nhiệt chấp nhận mô hình này để chứng minh sự hiện hữu của Thượng đế. Định kiến và sự khước từ số Không cùng với cái Không của Aristotle có thể cũng chưa là một trở ngại bất khả vượt qua; tuy nhiên khi kết hợp định kiến này với quyền lực của giáo hội Thiên Chúa giáo thời Trung cổ, thì nó trở thành một sức mạnh vô song. Quyền lực của giáo hội chi phối tất cả mọi sinh hoạt của Âu châu và đức Giáo hoàng được coi là bất khả ngộ (infallible) (Arnold, 1999). Một khi giáo hội đã chấp nhận mô hình của Aristotle-Ptolemy thì nó trở thành bất khả tư nghị.

Mô hình địa tâm được chấp nhận có nghĩa là số Không và cái Không bị từ khước và tẩy chay khỏi Âu châu, và cũng vì vậy, trên phương diện toán học, thiên văn, và hình học, Âu châu bị dậm chân tại chỗ không thoát ra khỏi trình độ số học và hình học Euclid, tính toán thì theo hệ thống số rắc rối của La-mã, kéo dài từ thế kỷ thứ tư đến thế kỷ thứ 12 (Mastin, 2010).

Mãi cho đến thế kỷ 13, số Không mới xuất hiện ở Âu châu, nhờ ở sự giao thương giữa Đông phương và Tây phương. Những thương gia Ấn-độ và Ả-rập mang theo với họ con số Không qua Âu châu, và Leonardo de Pisa[7] (Chàng Leonardo xứ Pisa), còn được biết đến là Fibonacci,[8] qua tác phẩm “Kế Toán Thư” (Liber Abaci) xuất bản năm 1202, giới thiệu con số Không, cùng với hệ thống số Ấn-độ Ả-rập và những tiện lợi của hệ thống số này, đến với nền toán học Tây phương (Mastin, 2010). Mặc dầu hệ thống số Ả-rập đã chứng tỏ được sự ưu việt so với hệ thống số La-mã, mãi đến thế kỷ 16, hệ thống số Ân-Ả-rập mới được áp dụng và phổ biến tại Tây phương (Mastin). Cũng sang thế kỷ 16, Copernicus, một nhà thiên văn học người Ba-lan, đề xướng mô hình nhật tâm (heliocentrism) với tác phẩm De Revolutionibus ấn hành năm 1543 khi ông sắp lìa đời, và mô hình nhật tâm đã đánh đổ hoàn toàn mô hình địa tâm của Aristotle và Ptolemy (Seife, 2000). Khi số Không và mô hình nhật tâm được chấp nhận tại Âu châu, ta thấy một sự nở rộ về học thuật trên mọi phương diện.

Số Không bị khước từ tại Tây phương chỉ vì một bộ óc, có thể nói là một trong những bộ óc siêu tuyệt nhất của nhân loại, không chấp nhận nó. Hệ quả của sự đóng cứng não trạng này là hai ngàn năm “tăm tối.”[9] Và qua số phận của số Không, ta thấy ngay cả bộ óc vĩ đại nhất cũng phạm sai lầm. Sau thời kỳ “hắc ám” là thời kỳ “phục hưng” và “khai sáng.” Những nhà tư tưởng của thời đại sau này đã xiển dương chủ nghĩa duy nghiệm (empiricism), theo đó những định luật (khoa học), những “chân lý” chỉ là những giả thuyết, tức là sự giải thích tạm thời đã được kiểm chứng (Trần Bích Lan, 1967). “Chân lý” hôm nay có thể bị phủ nhận ngày mai. Điều này tuy khiến ta có thái độ hoài nghi, nhưng đó là thái độ hoài nghi lành mạnh (healthy skepticism) để không đi đến chỗ cực đoan và đóng cứng não trạng.

Chủ nghĩa duy nghiệm có thể được xem là một phương thuốc nhằm giải cái độc “đóng cứng não trạng,” và đã được lần lượt những bộ óc kiệt xuất của thời đại khai sáng như Francis Bacon, John Locke, David Hume, và John S. Mill, xây dựng và phát triển thành một hệ thống suy nghiệm hoàn chỉnh, với những ứng dụng trong khoa học và toán học. Về toán học phải kể đến Descartes với trục toạ độ (0, 0) cùng sự phối hợp đại số với hình học thành môn hình học giải tích của ông (thế kỷ 16); rồi đến môn giải tích và vi phân do Newton và Leibniz sáng tạo. Về phương diện khoa học, thì Newton phải được coi là một “người khổng lồ” với những định luật về cơ học, và nhiệt học.

Về phương diện tư tưởng, Mill chủ trương là con người phải có quyền tự do tư tưởng vì những lẽ sau đây: thứ nhất, tư tưởng được công luận chấp nhận có thể sai (như mô hình điạ tâm); thứ hai, không những công luận có thể sai, mà ngay cả khi đúng chăng nữa, nếu không được tranh luận tự do, thì cái “công luận đúng” đó sẽ trở thành giáo điều chết. Nếu “sự thật” bị chết thành định kiến, thì chẳng ai còn để ý đến nữa và sẽ bị thui chột. Thứ đến, khi có hai lý thuyết trái ngược nhau thì “sự thật” chưa hẳn thuộc về một lý thuyết nào mà có thể nằm ở một khoảng nào ở giữa, hay mỗi bên đều có một phần sự thật; cho nên, nếu không có tranh luận, phần sự thật đó có thể bị mất và là một phần thiệt thòi cho nhân loại (Mill, bản dịch Việt ngữ Dương Văn Hoá, 2014).

Trong thế kỷ 20 ta cũng đã từng chứng kiến cái gọi là “chủ nghĩa siêu việt,” là “đỉnh cao trí tuệ,” là “bất khả ngộ” ở Liên bang Xô-viết và ở những nước cộng sản; đảng cộng sản đã dùng bạo lực để bóp nghẹt mọi tư tưởng khác biệt và đã đưa nhân loại đi vào một giai đoạn đen tối khác, nhưng may thay chỉ chưa đầy một trăm năm, thực tế khách quan đã chứng minh được sự sai lầm khốc hại của những chủ nghĩa không tưởng như vậy, và chúng đã bị đào thải. Trên phương diện quốc tế, sự đóng cứng não trạng, trong thế kỷ 20, không những gây ra sự đóng băng tư tưởng tại những nước kể trên, mà còn gây ra những tội ác kinh khủng chống lại nhân loại, như vụ diệt chủng của Khmer Đỏ tại Kampuchia, Đại Nhẩy vọt và Cách mạng Văn hoá  của Mao Trạch Đông tại Trung Hoa, và những cuộc đại thanh trừng của Stalin tại  Xô-viết. Âu châu còn chịu đựng thêm một thảm trạng nữa của sự đóng cứng não trạng khi Đức Quốc Xã tiến hành cuộc diệt chủng hàng triệu người chỉ vì niềm tin là giống dân Aryan là “siêu nhân” và có nhiệm vụ thống trị nhân loại.

Mặc dù chủ nghĩa Duy nghiệm đã chứng tỏ là hữu hiệu trên phương diện nghiên cứu khoa học, nhưng còn trên phương diện cá nhân, liệu chúng ta có học được những bài học của lịch sử, từ thời cổ đại đến cận đại, về sự nguy hại của sự đóng cứng não trạng hay định kiến hay không? Làm thế nào để giải thoát được khỏi những định kiến bó chặt tư tưởng của ta và của những người khác? Đó vẫn là một bài toán nan giải, như Einstein đã nói: “Phá vỡ định kiến của con người còn khó hơn là phá vỡ hạt nhân nguyên tử.”

Kết luận

Con người từ 30,000 năm trước đã biết đếm và đã phát minh ra những hệ thống số khác nhau, từ khu vực Lưỡng Hà sang đến Âu châu, rồi Á châu. Thế nhưng trong những hệ thống số này hoàn toàn vắng bóng con số Không, và cả khái niệm về cái “Không.” Mãi cho đến thế kỷ thứ năm TCN, số Không mới được các nhà toán học và thiên văn học Ấn-độ sử dụng, và số Không cùng cái “không” và cái “vô cùng” được người Á châu chấp nhận trong triết học, toán học, và tôn giáo. Trong khi đó Tây phương từ khước số Không và cái “không” vì hai khái niệm này đi ngược lại với quan niệm về vũ trụ của họ, một vũ trụ hữu hạn, với trái đất là trung tâm của vũ trụ, và nó đứng yên. Niềm tin vào mô hình địa tâm do Aristotle đề xướng đã đóng cứng não trạng của những nhà khoa học thời cổ sang tới thời Trung cổ trong suốt 2000 năm. Mãi cho đến thế kỷ 13 khi giao lưu văn hoá và thương mại giữa Đông và Tây phương được thiết lập, số Không được du nhập vào Âu châu nhưng cũng phải mất thêm ba thế kỷ nữa, hệ thống số Ả-rập như ta dùng ngày nay mới được chấp nhận và sử dụng. Thêm vào đó, mô hình vũ trụ nhật tâm (thái dương hệ) của Copernicus đã xô đổ mô hình địa tâm của Aristotle và mở đường cho Âu châu đi vào thời kỳ Khai Sáng với những thành quả và tiến bộ về khoa học, triết học, và toán học như ta biết ngày nay. Sự đóng cứng của não trạng dẫn đến sự đóng băng tiến hoá. Người viết xin mượn lời của Frank Zappa để kết thúc tiểu luận này: “Tâm trí con người cũng giống như một cánh dù. Nó chỉ xài được khi được mở ra.”

Nông Duy Trường

© Học Viện Công Dân, Oct 2015

Tài liệu tham khảo

Arnold, J. (1999). The roman catholic church of the middle ages. Retrieved July 10, 2015 from http://www.thirdmill.org/newfiles/jac_arnold/CH.Arnold.RMT.1.html

Clegg, B. (2011). NRICH Mathematics http://nrich.maths.org/2671/index

Conant, L. (1896). The Number Concept. (Lit2Go ed.). Retrieved July 01, 2015, from http://etc.usf.edu/lit2go/219/the-number-concept/

Liu, JL., & Berger, D. (2014). Nothingness in Asian philosophy. New York, NY: Routledge.

Mark, J. (2013). Acient egyptian mythology. Retrieved August 12, 2015, from http://www.ancient.eu/Egyptian_Mythology/

Mastin, L. (2009). Cosmological theories through history. Retrieved September 10, 2015, from http://www.physicsoftheuniverse.com/cosmological.html

Mastin, L. (2010). The story of mathematics. Retrieved September 10, 2015, from http://www.storyofmathematics.com/medieval.html

Nguyễn, Bách T. (2006). Lưới trời ai dệt. Saigon: Nhà Xuất bản Trẻ.

 O’Connor, J. & Robertson, E. Pythagoras of Samos. (1999). Retrieved July 10, 2015 http://www-history.mcs.st-andrews.ac.uk/Biographies/Pythagoras.html

Seife, C.(2000). Zero: The biography of a dangerous idea. New York, NY: Penguin, Putnam.

Trần, Lan B. (1967). Luận lý học. Sài Gòn: Nhà Xuất bản Ngôn Ngữ.

Weibull, N. (2014): An historical survey of number systems. RetrievedJuly 10, 2015, from

http://www.math.chalmers.se/Math/Grundutb/GU/MAN250/S04/Number_Systems.pdf

Danh sách các hình

Hình 1: Số Sumerian; nguồn http://www.ancientscripts.com/sumerian.html

Hình 2: Số Hy-lạp; nguồn http://forwardcurves.com/?id=662

Hình 3: Số Maya; nguồn https://sites.google.com/site/culturasprehispanicas/losmayas

Hình 4: Số Ấn-Ả-rập; nguồn https://www.mathsisfun.com/definitions/hindu-arabic-number-system.html

Hình 5: Mô hình địa tâm; nguồn http://www.the-universe.ie/aristotle’s-universe.html

[1] Số 1 trong chữ số tượng hình của Ai-cập là một vạch thẳng đứng. Số 100.000 là hình con cóc hay con chim.

[2] Thales (624 TCN- 547 TCN) và Pythagoras (569 TCN- 475 TCN) đã có những định lý hình học nổi tiếng mà bất cứ một học sinh trung học nào cũng phải biết.

[3] Bốn trăm năm sau, vào thế kỷ thứ nhất, Kinh thánh Tân ước được viết ra, và trong sách John, 1:1 có nói: “Từ thuở thái sơ đã có Ngôi Lời (logos/ratio), Ngôi Lời ở với Đức Chúa Trời, và Ngôi Lời là Đức Chúa Trời.”

[4] Giả sử ta có một đoạn thằng với chiều dài bằng một đơn vị, và x là chiều dài của phần nhỏ. Phần dài hơn sẽ là 1-x. Tỷ lệ sẽ là x/(1-x) = (1-x)/1

[5] Ấn giáo (Hinduism) được xem là tôn giáo cổ nhất nhân loại, phát xuất từ Ấn-độ khoảng 5000 TCN. Phật giáo bắt đầu khoảng thế kỷ thứ năm TCN. Đạo giáo (Taoism) bắt đầu khoảng thế kỷ thứ tư TCN.

[6] Aristotle, nhà bác học của cổ Hy-lạp, tư tưởng Aristotle vẫn còn ảnh hưởng cho đến nay về phương diện triết học, đạo đức, khoa học, giáo dục, y khoa, v.v. Aristotle sáng lập trường Lyceum, và là người đầu tiên phân định các ngành học và môn học như ta biết: văn chương, triết, toán, khoa học, thiên văn, sinh vật. Lyceum được coi là một đại học nghiên cứu (research university) hiểu theo nghĩa ngày nay.

[7] Pisa là một thành phố thuộc Tuscany, miền Trung nước Ý, nơi có ngọn tháp nghiêng nổi tiếng.

[8] Fibonacci, tức Leonardo de Pisa, nhà toán học nổi tiếng thời Trung cổ với dãy số Fibonacci. Dãy số này vẫn thường được minh hoạ bằng sự sinh sản của những cặp thỏ như sau: vào tháng 0, bỏ một cặp thỏ đực và cái ở chung với nhau (1 cặp). Sang tháng 1, cặp thỏ này vẫn chưa sinh sản (1 cặp); sang tháng 2, cặp thỏ này sinh một cặp thỏ con (2 cặp); sang tháng 3, cặp thỏ đầu tiên sinh cặp thứ hai (cặp thứ ba chưa sinh sản được) (3 cặp); tiến trình cứ thế tiếp diễn, sang đến tháng 4 có 5 cặp, …Dãy số trở thành 1, 1, 2, 3, 5, 8,…Điều kỳ lạ là dãy số này thể hiện trong những hiện tượng thiên nhiên như những mắt trái khóm, hay trái thông, và tỷ lệ những con số với số đứng trước càng lúc càng tiến gần tỷ số vàng.

[9] Thời Trung cổ còn được gọi là thời đại tối tăm (Dark Ages) vì không có những đóng góp gì đáng kể cho nền văn minh của Âu châu (Nguyễn Tường Bách, 2006).